$\parbox{10cm}{\scriptsize Université René Descartes -- Paris 5 \\ {... ...thématiques et Informatique}\\ 45, rue des Saints-Pères 75270 Paris cedex 06 }$

Licence 1^re année, 2005-2006

Environnement de calcul scientifique

Contrôle continu du 11 mai 2006

Les exercices correspondent, à l'ordre près, à ceux posés au contrôle.

Les réponses correctes sont indiquées par .

Exercice 1.

Les lignes proposées sont écrites dans un éditeur et sauvegardées dans un fichier intitulé f.sci. On utilise ensuite la command getf("f.sci"). Cela permet de définir une fonction qui, à deux vecteurs lignes v et w de taille n, associe la matrice carrée A, de taille [n,n], telle que A(i,j) = v(j) si i est impair et A(i,j) = w(j) si i est pair.

:	function A=f(v,w)
	n=size(v,"c");
	A=ones(v')*v;
	for i=2:2:n, A(i,:) = w; end;
	endfunction
:	function A=f(v,w)
	n=size(v,"c");
	A=zeros(n,n);
	for i=1:2:n, A(i,:) = v; end;
	for i=2:2:n, A(i,:) = w; end;
	endfunction
C :	function A=f(v,w)
	n=size(v,"c");
	A=ones(v').*v;
	for i=2:2:n, A(i,:) = w; end;
	endfunction
D :	function A=f(v,w)
	A=[];
	n=size(v,"c");
	for i=1:2:n, A = [A,v,w]; end;
	endfunction
E :	function A=f(v,w)
	n=size(v,"c");
	for i=1:n, A = [A,v',w']; end;
	endfunction

(1/4)

Exercice 2.

Les lignes proposées sont écrites dans un éditeur et sauvegardées dans un fichier intitulé f.sci. On utilise ensuite la command getf("f.sci"). Cela permet de définir une fonction qui, à une matrice A et un nombre b, associe la matrice C telle que C(i,j) = max(A(i,j),b).

:	function C=f(A,b)
	C=max(A,b*ones(A));
	endfunction
:	function C=f(A,b)
	n=size(A);
	C=zeros(A);
	for i=1:n(1), for j=1:n(2),
	if A(i,j)>b then, C(i,j)=A(i,j);
	else C(i,j)=b;
	end; end; end;
	endfunction
C :	function C=f( A,b)
	max(A,b*ones(A));
	endfunction
D :	C=max(A,b*ones(A))
E :	function C=f(A,b)
	C = zeros(A);
	bool = A > b;
	C(bool) = A(bool);
	endfunction

Exercice 3.

Les opérations suivantes définissent la fonction moyenne qui, à deux vecteurs lignes v et w de taille n, associe le vecteur ligne u de taille n tel que u(i) = (v(i)+w(i))/2.

:	Sauver dans le fichier f.sci les lignes
	function u=moyenne(v,w)
	u=(v+w)/2;
	endfunction
	puis charger le fichier par getf("f.sci")
:	Sauver dans le fichier f.sce la ligne
	deff("u=moyenne(v,w)","u=(v+w)/2")
	puis charger le fichier par exec("f.sce")
C :	Sauver dans le fichier f.sci la ligne
	deff("u=moyenne(v,w)","u=(v+w)/2")
	puis charger le fichier par getf("f.sci")
D :	Sauver dans le fichier f.sci les lignes
	function u=f(v,w)
	u=(v+w)/2;
	endfunction
	puis charger le fichier par getf("f.sci")
E :	Sauver dans le fichier f.sci les lignes
	function u=moyenne(v,w)
	(v+w)/2;
	endfunction
	puis charger le fichier par exec("f.sci")

(2/4)

Exercice 4.

Soit A=rand(3,3). La ligne de commande suivante affiche un message d'erreur :

: A(3,1)=[]

: A<rand(2,2)

C : A^2

D : A(2,:)=[]

E : A<0

Exercice 5.

Soient v=rand(1,3) et w=rand(3,1). La ligne de commande proposée affiche une matrice de taille 3x3 :

: w*v

: v'*ones(v)+ones(w')*w

C : v*w

D : w.*v

E : toeplitz(zeros(v),ones(w))

Exercice 6.

Les lignes de commande suivantes affichent une représentation graphique correcte de la fonction:
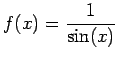$f(x)= \displaystyle \frac{1}{\sin(x)}$, pour $x\in ]-\pi,+\pi[$ :

: e=0.1; x=linspace(e,%pi-e,200); x=[x'-%pi,x']; y=(1)./sin(x); plot2d(x,y,[5,5]);

: x=[0.1:0.01:%pi-0.1]'; y=(1)./sin(x); plot2d([x-%pi,x],[-y,y],[5,5]);

C : x=[0:0.001:%pi]; x=[x'-%pi,x']; y=(1)./sin(x); plot2d(x,y,[5,5]);

D : x=[-%pi:%pi]; y=(1)./sin(x); plot2d(x,y);

E : x=[-%pi+0.1:0.1:%pi-0.1]; y=1/sin(x); plot2d(x,y);

Exercice 7.

La ligne de commande suivante :
x=linspace(-%pi,%pi,50)'; y=[sin(-x),zeros(50,1),sin(x)]; plot2d([x,x,x],y,[1,2,3]);

: trace les courbes $y=\sin(-x)$, $y=0$ et $y=\sin(x)$ avec des couleurs différentes.

: donne le même résultat que :

x=linspace(-%pi,%pi,50)'; y=[]; for i=-1:1, y=[y,sin(x.*i)]; end; plot2d([x,x,x],y);

C : trace les courbes $y=\sin(-x)$, $y=0$ et $y=\sin(x)$ avec la même couleur.

D : renvoie un message d'erreur.

E : ne trace que la courbe $y=\sin(x)$.

Exercice 8.

La ligne de commande suivante affiche une valeur numérique proche de $\int_0^{10}\sqrt{t}\, dt$ :

: integrate("sqrt(x)","x",0,10)

: t=[0:0.001:10]; inttrap(t,sqrt(t))

C : t=[0, 10]; inttrap(t,sqrt(t))

D : t=[0:0.001:10]; cumsum(sqrt(t))

E : t=[0:0.001:10]; sum(sqrt(t)/0.001)

(3/4)

Exercice 9.

On pose A=[1:4;4:-1:1;0:3] et v=[2;2;3] :

: v(3:-1:1)==A(:,3) donne [T T T]'

: v*v' est une matrice à trois lignes et trois colonnes.

C : v(3:-1:1)'==A(3,:) donne [T T T]

D : v'*A*v est un réel.

E : B=A'; B(:,3)==v donne [T T T]

Exercice 10.

Soit A=[0:3;3:-1:0]+%i*[1:4;4:-1:1]. La ligne de commande proposée affiche une matrice réelle ou complexe à deux lignes et quatre colonnes :

: real(A)

: abs(A)

C : A'

D : imag(A);

E : real(A)<imag(A)

(4/4)