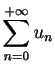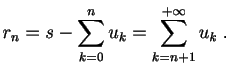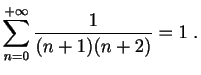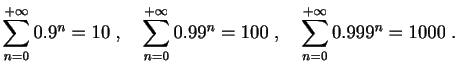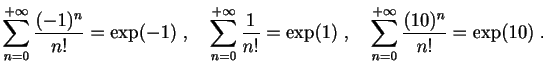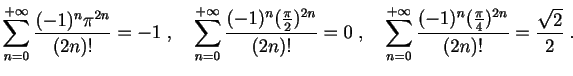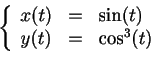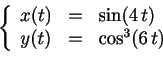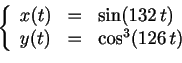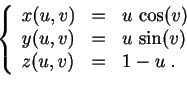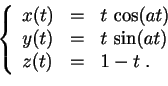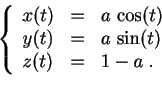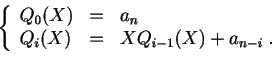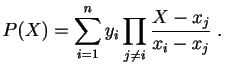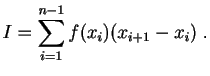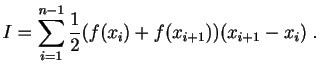- Nombres de
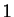 à
à 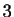 par pas de
par pas de 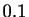 .
.
- Nombres de
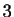 à
à 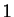 par pas de
par pas de 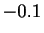 .
.
- Carrés des
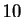 premiers entiers.
premiers entiers.
- Nombres de la forme
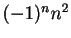 pour
pour
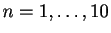 .
.
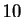 ``0
'' suivis de
``0
'' suivis de 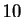 ``
``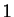 ''.
''.
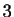 ``0
'' suivis de
``0
'' suivis de 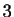 ``
``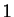 '', suivis de
'', suivis de 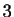 ``
``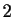 '',...,
suivis de
'',...,
suivis de 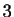 ``
``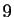 ''.
''.
- ``
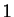 '', suivi de
'', suivi de 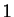 ``0'', suivi de ``2'', suivi de 2 ``0
'',...
, suivi de ``
``0'', suivi de ``2'', suivi de 2 ``0
'',...
, suivi de ``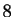 '', suivi de
'', suivi de 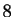 zéros, suivi de ``
zéros, suivi de ``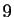 ''.
''.
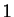 ``
``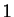 '' suivi de
'' suivi de 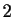 ``
``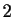 '', suivis de
'', suivis de 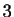 ``
``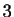 '',...,
suivis de
'',...,
suivis de 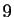 ``
``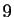 ''.
''.