Corrigé du devoir

Questions de cours :

Il y a deux erreurs dans le calcul de y. D'une part, la commande correcte est y=x.*sin((1)./x). D'autre part, si n est impair, le vecteur x contient 0 et le calcul de y renvoie un message de division par 0 . En outre, les variations de 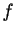sont beaucoup plus importantes au voisinage de 0 . Définir un vecteur d'abscisses régulièrement espacées, même grand, ne permet pas de zoomer en conservant la même qualité de représentation au voisinage de 0 .
```
h=0.1; uh = 1/h;
x = %pi*[floor(uh/%pi):0.1:ceil(uh*1000/%pi)]; x(1)=[];
X = (1)./x;                       
Y = X.*sin(x);                     
clf();
plot2d(X,Y);
```
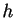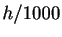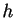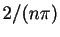Le vecteur des abscisses X a pour valeurs extrêmes des valeurs proches de et (si est petit). Les valeurs sont de plus en plus concentrées au voisinage de 0 , de plus les abscisses de la forme $2/(n\pi)$ figurent dans le vecteur, donnant une représentation qui respecte les maxima et minima locaux de .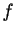
Du fait de la parité de la fonction 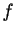, il suffit de représenter les abscisses opposées avec les mêmes ordonnés.
La représentation peut se faire sur le carré $[-h\,;\,+h]^2$ .

function y=xsin1(h)
//
//   Represente le graphe de la fonction y=x*sin(1/x) 
//   entre -h et h. Retourne la valeur en h.
//
uh = 1/h;
y = h*sin(uh);                     
x = %pi*[floor(uh/%pi):0.1:ceil(uh*1000/%pi)]; x(1)=[];
X = (1)./x;                       
Y = X.*sin(x);                     
clf();
plot2d(-X,Y,style=5,rect=[-h,-h,h,h],nax=[1,10,1,10]);
plot2d([-X($),0,X($)],[Y($),0,Y($)],style=5,frameflag=0);  // relie parties paires et impaires
plot2d(X,Y,style=5,frameflag=0);
endfunction

Exercice 1 :

function D=differences_divisees(x,y)
//
//     Calcule la matrice des differences divisees
//     du vecteur y par le vecteur x (vecteurs lignes).
//
d = y; D=[d];                // initialisation
n=size(y,"*");               // taille du vecteur
for i=1:n-1,                 // construction des lignes
   dy = d(2:n-i+1)-d(1:n-i); // differences d'ordonnees
   dx = x(1+i:n)-x(1:n-i);   // differences d'abscisses
   d = dy./dx;               // differences divisees
   D=[D;d,zeros(1,i)];       // stocker le resultat  
end;
endfunction

x=gsort(rand(1,10),"c","i"); y=x.^5+3*x^4-2*x^2+x-1;
D=differences_divisees(x,y)

function P = Newton(x,y)
//
//     Retourne le polynome d'interpolation 
//     des valeurs y aux points x
//     (x et y sont deux vecteurs lignes de meme taille).
//     Le calcul utilise les differences divisees.
//
n = size(x,"*");               // nombre de points
d = y;                         // differences divisees 
s = n;                         // longueur
P = y(1);                      // initialisation du polynome
f = 1;                         // produit de facteurs 
for k=1:n-1,
   d = d([2:s])-d([1:s-1]);    // nouveau vecteur de differences
   a = x([n-s+2:n])-x([1:s-1]);// differences d'abscisses
   d = d./a;                   // diviser par les differences
   s = s-1;                    // la taille diminue
   f = f*(%s-x(k));            // nouveau produit
   P = P+d(1)*f;               // ajouter au polynome
end;
endfunction

x=gsort(rand(1,5),"c","i"); y=x.^5+3*x^4-2*x^2+x-1;
P=Newton(x,y); horner(P,x)-y

function P = Lagrange(x,y)
//
//     Retourne le polynome d'interpolation 
//     des valeurs y aux points x
//     (x et y sont deux vecteurs lignes de meme taille).
//     Le calcul utilise les polynomes cardinaux.
//
n = size(x,"*");               // nombre de points
P = 0;                         // initialisation du polynome
for k=1:n                      // parcourir les abscisses
   z = x;                      // recopier le vecteur d'abscisses
   z(k)=[];                    // supprimer la k-ieme
   L = prod((%s-z)./(x(k)-z)); // k-ieme polynome cardinal
   P = P+y(k)*L;               // multiplier par la valeur et ajouter
end;
endfunction

x=gsort(rand(1,1000),"c","i"); y=rand(1,1000);
timer(); Newton(x,y); tN=timer()
timer(); Lagrange(x,y); tL=timer()

x=gsort(rand(1,10),"c","i"); c=rand(1,10); 
P=poly(c,"X","coeff"); y=horner(P,x);
PN=Newton(x,y); norm(coeff(PN)-c)
PL=Lagrange(x,y); norm(coeff(PL)-c)

Exercice 2 :

deff("L=Lt(n)","L=toeplitz([1:n],[1,zeros(1,n-1)])")

```
deff("L=Lr(n)","L=tril(rand(n,n))")
```
```
n=100; L=Lt(n); A=L*L'; 
timer(); d=norm(L-chol(A)'); t=timer(); [d,t]
```
Avec Lt, les matrices L et A sont à valeurs entières. La décomposition de Cholesky est numériquement stable : la norme de la différence est nulle, même pour de grandes valeurs de 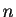. Le temps d'exécution observé (dépendant de la machine) est de l'ordre de 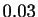s pour 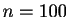, 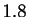s pour .
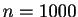Avec Lr, la décomposition de Cholesky est numériquement instable : la norme de la différence peut être très variable. Un message d'erreur sur le fait que la matrice A n'est pas définie positive peut apparaître dès .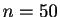

function L = Cholesky3(A)
//
//      Pour une matrice symetrique A, la matrice L
//      est triangulaire inferieure et A=L*L'
//      3 boucles emboitees. 
//
L=zeros(A);             // initialisation : matrice nulle
n = size(A,"r");        // nombre de lignes 
dia = sqrt(A(1,1));     // coefficient diagonal
L(:,1) = A(:,1)/dia;    // premiere colonne

for j=2:(n-1),          // colonnes suivantes
   dia = A(j,j);
   for l=1:(j-1),
      dia = dia - L(j,l)^2;
   end;
   dia = sqrt(dia); 
   L(j,j) = dia;        // coefficient diagonal
   for i=(j+1):n,
       aux = A(i,j);
       for l=1:(j-1),
          aux = aux - L(i,l)*L(j,l);
       end;
       aux = aux/dia;
       L(i,j) = aux; 
   end;
end;

dia = A(n,n);
for l=1:(n-1),
   dia = dia -L(n,l)^2;
end;
dia = sqrt(dia);
L(n,n) = dia;           // dernier coefficient 
endfunction

Les mêmes propriétés de stabilité ou instabilité numérique sont observées, le temps d'exécution est de 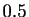s pour 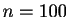, 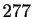s pour .

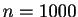function L = Cholesky2(A)
//
//      Pour une matrice symetrique A, la matrice L
//      est triangulaire inferieure et A=L*L'
//      2 boucles emboitees. 
//
L=zeros(A);             // initialisation : matrice nulle
n = size(A,"r");        // nombre de lignes 
dia = sqrt(A(1,1));     // coefficient diagonal
L(:,1) = A(:,1)/dia;    // premiere colonne

for j=2:n-1,            // colonnes suivantes
   dia = sqrt(A(j,j)-sum(L(j,[1:j-1]).^2));
   L(j,j) = dia;        // coefficient diagonal  
   for i=j+1:n,
       L(i,j) = (A(i,j) - sum(L(i,[1:j-1]).*L(j,[1:j-1])))/dia; 
   end;
end;

dia = sqrt(A(n,n)-sum(L(n,[1:n-1]).^2));
L(n,n) = dia;           // dernier coefficient 
endfunction

Le temps d'exécution est de 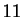s pour .

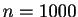function L = Cholesky1(A)
//
//      Pour une matrice symetrique A, la matrice L
//      est triangulaire inferieure et A=L*L'
//      1 seule boucle. 
//
L=zeros(A);             // initialisation : matrice nulle
n = size(A,"r");        // nombre de lignes 
dia = sqrt(A(1,1));     // coefficient diagonal
L(:,1) = A(:,1)/dia;    // premiere colonne

for j=2:n-1,            // colonnes suivantes
   dia = sqrt(A(j,j)-sum(L(j,[1:j-1]).^2));
   L(j,j) = dia;        // coefficient diagonal
   L([j+1:n],j) = (A([j+1:n],j) - ..
     sum(L([j+1:n],[1:j-1]).*(ones(n-j,1)*L(j,[1:j-1])),"c"))/dia;
end;

dia = sqrt(A(n,n)-sum(L(n,[1:n-1]).^2));
L(n,n) = dia;           // dernier coefficient 
endfunction

Le temps d'exécution est de 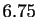s pour .

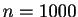2012-2013