
| Université René Descartes |
| UFR Mathématiques et Informatique |
| 2004-2005 |
| Licence 1ère année, UE MC1 |
|---|
(a) Pour chaque question du questionnaire à choix multiples, quatre réponses
sont proposées : deux réponses sont exactes et deux réponses sont fausses. L'étudiant
répondra en cochant, sur la feuille de réponse jointe à l'énoncé, les deux cases des
réponses qu'il pense correctes. Les points ne seront accordés que si les deux réponses
correctes, et elles seules, ont été cochées. Aucun point ne sera accordé si une seule
réponse, même
correcte, est cochée. La feuille de réponse ne doit pas être raturée.
Tout document est interdit. Les calculatrices et les téléphones portables,
même à titre d'horloge, sont également interdits.
![]() On considère
On considère

 .
.
![]()
 .
.
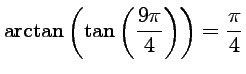 .
.
 .
.
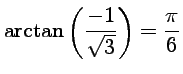 .
.
![]() On considère, dans
On considère, dans
![]() , la famille de vecteurs
, la famille de vecteurs
![]() .
.
![]() On considère, dans
On considère, dans
![]() , les
sous-ensembles :
, les
sous-ensembles :

![]() On considère les matrices :
On considère les matrices :
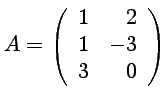 ,
,
 et
et

 .
.
 .
.
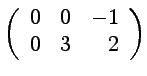 .
.
![]() On considère l'endomorphisme
On considère l'endomorphisme ![]() de
de
![]() défini par
défini par
![]() .
.
![]() Soit
Soit ![]() définie par
définie par

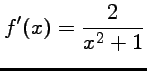 .
.
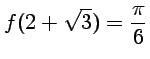 .
.
 .
.
![]() Soit
Soit ![]() définie par
définie par

 est un développement limité de
est un développement limité de

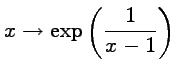 est la composée de l'exponentielle,
qui est de classe
est la composée de l'exponentielle,
qui est de classe
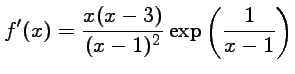
 tend vers
tend vers
Quand ![]() tend vers 1 en restant inférieur à 1 (à gauche),
tend vers 1 en restant inférieur à 1 (à gauche),
![]() tend vers 0 en restant négatif,
tend vers 0 en restant négatif,
 tend vers
tend vers ![]() et donc l'exponentielle tend vers 0. Le
polynôme
et donc l'exponentielle tend vers 0. Le
polynôme ![]() tend vers 2. Par produit de ces limites, la limite de
tend vers 2. Par produit de ces limites, la limite de ![]() à gauche de 1 existe et est
égale à 0
.
à gauche de 1 existe et est
égale à 0
.
Les limites à gauche et à droite n'étant pas égales, ![]() n'a pas de
limite en 1.
n'a pas de
limite en 1.
 donc
donc
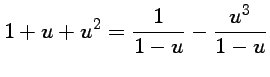 ou encore
ou encore
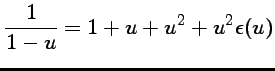 qui est un
développement limité à l'ordre 2 en 0 de
qui est un
développement limité à l'ordre 2 en 0 de
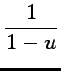 . Il suffit ensuite de multiplier par
. Il suffit ensuite de multiplier par
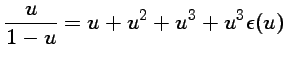

pour un

qui est le développement limité à l'ordre 3 en 0 de l'exponentielle.

et on ne garde que les puissances inférieures ou égales à 3 :

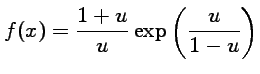 . Il suffit donc de multiplier le
développement limité précédent par la fraction :
. Il suffit donc de multiplier le
développement limité précédent par la fraction :



