Non local approaches for image denoising
Table des matières
For the following exercices, you need Matlab.
The subject of these exercices is patch-based image denoising. Assume that we observe a noisy \(n\times n\) image $$v = u + b,$$ with \(b\) an additive gaussian noise (assumed to be i.i.d \(\mathcal N (0,\sigma^2)\)). Our goal is to recover \(u\) from the values of \(v\). Non local methods try to solve the inverse problem of recovering \(u\) from \(v\) by performing some kind of regularization in the patch space. Patches are small images extracted from \(v\). In the following we will consider square patches of size \((2f+1)\times (2f+1)\).
Start by creating the noisy image \(v\) by adding a gaussian noise image to an known image \(u\).
s = 20 % noise standard deviation u = double(imread('im/simpson_nb512.png')); v = u+s*randn(size(u)); % use grand(u,"nor",0,s) with Scilab figure(1);imshow(v,[]); % display v

Figure 1 : image u

Figure 2 : same image with an additive gaussian noise of standard deviation 20
Be careful with the function imshow(). If u is an image encoded in double, imshow(u) will display all values above 1 in white and all values below 0 in black. If the image u is encoded on 8 bits though, imshow(u) will display 0 in black and 255 in white. In order to scale u and use the full colormap, use the command imshow(u,[]).
1 Patch extraction and image reconstruction
1.1 Patch extraction
The first step of a patch-based restoration method consists in extracting all sliding patches from the degraded image \(v\). Patches here are all square images of size \((2f+1)\times (2f+1)\) (for instance \(7\times 7\) if \(f = 3\)) extracted from \(v\). In Matlab / Scilab, for a given image \(v\), the patch of coordinates \((i,j)\) and size \((2f+1)\times (2f+1)\) is given by $$u(i-f:i+f,j-f:j+f).$$
In Matlab, you can use the function im2col to extract all image patches and rearrange them into columns into a huge matrix. Beware of the fact that the obtained matrix will have \((2f+1)\times (2f+1)\) lines but only \((n-2*f)\times(m-2*f)\) columns since only patches completely included in \(v\) are extracted.
Matlab
Y = im2col(v,[2*f+1 2*f+1],'sliding');
1.2 Image reconstruction
The goal of the following sections is to study several methods to denoise the patches in the matrix \(Y\). Once the matrix \(Y\) is denoised into \(Ydenoised\), there are several ways to reconstruct the denoised image \(u\). First, we can simply extract a line \(k\) of \(Ydenoised\) (explain why) :
Matlab
vdenoised = reshape(Ydenoised(k,:),nr-2*f,nc-2*f);
Each line of \(Ydenoised\) yields a denoised version of \(v\) but shifted in space. In order to denoise \(v\) a little further, we can average all of these denoised versions, after correcting their relative shifts.
Matlab
tmp = zeros(nr,nc,(2*f+1)^2); nb = zeros(nr,nc); for x = 1:2*f+1 for y = 1:2*f+1 i = (2*f+1) *(y-1)+x; w = reshape(Y(i,:),nr-2*f,nc-2*f); % use matrix instead of reshape in scilab tmp(x:nr-2*f+x-1,y:nc-2*f+y-1,i) = w; nb(x:nr-2*f+x-1,y:nc-2*f+y-1) = nb(x:nr-2*f+x-1,y:nc-2*f+y-1) +1; end end vdenoised = sum(tmp,3)./nb;
- Explain the previous code. Try to decompose an image into its set of patches and to reconstruct it with the previous operations.
2 PCA-based denoising
This part is about PCA image denoising. It is inspired by the paper
C.-A. Deledalle and J. Salmon and A. Dalalyan, Image denoising with patch based PCA: local versus global, proceedings of BMVC 2011.
2.1 PCA
Once patches have been extracted, we consider them as a set of column vectors in \(\mathbb{R}^{(2f+1)^2}\) : \[Y = (Y_1,\dots,Y_{nm}).\] In order to remove the noise in \(v\), we propose to threshold these vectors in a well chosen orthogonal basis. This basis is learned by applying a PCA to the set of vectors \((Y_1,\dots,Y_{nm})\).
To this aim, we compute the mean vector \(mY\) and the covariance matrix \(C\) for this set of vectors : \[mY = \frac{1}{nm} \sum_{k=1}^{nm} Y_k, \;\; C = \frac{1}{nm} \sum_{k=1}^{nm} (Y_k-\bar{Y})(Y_k-\bar{Y})^t.\]
- Write a function [moy,C,Yc]=moyCov(Y) which computes the mean vector and covariance matrix of a set of column vectors \(Y=(Y_1,\dots,Y_{nm})\). The function should also provide the centered matrix \(Y_c = (Y_1-mY,\dots,Y_{nm}-mY)\).
Matlab
function [mY,C,Yc]=moyCov(Y) mY = C = INSERT YOUR CODE Yc =
Principal component analysis (PCA) consists in computing eigenvalues and eigenvectors of \(C\). More precisely, if \(\lambda_1 \geq \dots \geq \lambda_{(2f+1)^2}\) are eigenvalues of \(C\), and \(X_1,\dots,X_{(2f+1)^2}\) the corresponding (normalized) eigenvectors, we call \(X_k\) the \(k\)-th principal component of set of vectors \((Y_1,\dots,Y_{nm})\).
In this new basis \(X\), each vector \(Y_k\) can be rewritten as $$Y_k = m_Y + Y_k - m_Y = m_Y + \sum_{i=1}^{(2*f+1)^2} X_i^t(Y_k-m_Y) X_i.$$
- Compute and display the orthonormal basis \(X\) and the eigenvalues of the covariance matrix \(C\). Display the eigenvalues in decreasing order. You can use the function
eigof Matlab. The command
[X,D] = eig(C);
yields a diagonal matrix D of eigenvalues and a matrix X whose columns are the eigenvectors of C. Be careful that the eigenvalues in D are not ordered.
% plot eigenvalues in decreasing order [D,I] = sort(diag(D), 'descend'); plot(D); X = X(:,I); % plot first eigenvectors figure;colormap(gray); for i=1:25 subplot(5,5,i);imagesc(reshape(X(:,i),2*f+1,2*f+1));axis image; end
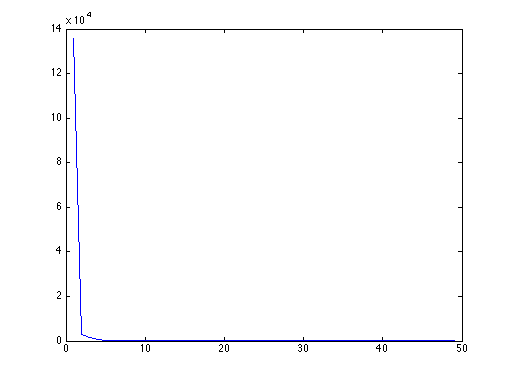
Figure 3 : eigenvalues of C in decreasing order
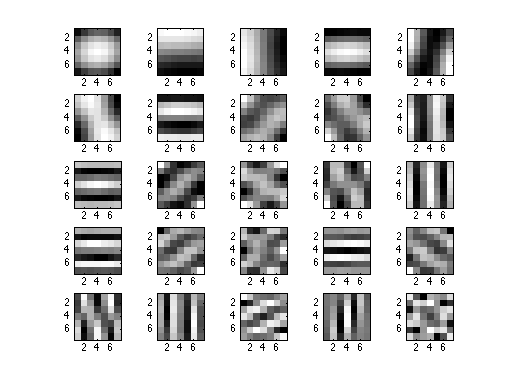
Figure 4 : 25 first eigenvectors of C
Hard thresholding In order to denoise \(Y_k\), we propose to threshold to \(0\) all coefficients \(X_i^t(Y_k-m_Y)\) smaller in norm that a given fixed threshold \(\eta\). We then construct a new matrix \(Z\) from \(Y\)
\begin{equation} Z_k = m_Y + \sum_{i=1}^{(2*f+1)^2} \phi\left(X_i^t(Y_k-m_Y)\right) X_i, \label{eq:seuilage} \end{equation}where \(\phi\) if the hard thresholding function
\begin{equation} \label{eq:seuillage_dur} \phi(t) = t.\mathbf{1}_{|t| > \eta}. \end{equation}If we note \(X\) the matrix of eigenvectors, this can be done easily with the following commands
Yproj=X'*Yc; % computation of all scalar products X_i^t(Y_k-m_Y) eta = 30; Yproj(abs(Yproj)<eta)=0; % hard thresholding Z = X*Yproj + mY*ones(1,size(Y,2)); % reconstruction of the patches after hard thresholding
- Write a function [Z]=debruitePCA(Y,eta) which computes the PCA of \(Y\) and apply the previous hard thresholding to its coefficients to denoise it.
Soft thresholding. The previous hard thresholding can be replaced by a smoother one, by replacing the function \(\phi\) by the function
\begin{equation} \psi(t) = sign(t)*\max(0,|t|-\eta) = (t-\eta) * \mathbf{1}_{t > \eta} + (t+\eta) * \mathbf{1}_{t <- \eta} \label{eq:seuillage_doux} \end{equation}- Write a function [Z]=debruitePCAdoux(Y,eta) which computes the PCA of \(Y\) and apply the previous soft thresholding to its coefficients to denoise it.
PCA + thresholding + reconstruction
We are now in the position to completely denoise an image, by applying the different steps studied above
- decomposition of \(v\) into patches \(Y\)
- PCA analysis of \(Y\), followed by hard of soft thresholding to obtain \(Z\)
- reconstruction of \(vdenoised\) from \(Z\)
.
- Test the whole method for several values of the noise standard deviation and several values of the threshold \(\eta\). In order to evaluate the obtained results, you can compute the \(L^2\) distance between the denoised image \(vdenoised\) and the (known) input image \(u\). Test the method for several images. Is there a link between the standard deviation of the additive noise and the optimal parameter \(\eta\) ?

Figure 5 : image restored by soft thresholding
2.2 Localization
The previous method use a unique orthonormal basis to represent all patches in the whole image. In this sense, the method can be considered as global. In order to better adapt to the local image geometry, the method can be applied locally, for instance by cutting the image \(v\) into rectangles.
- Write a function which cut your image into overlapping rectangles (for instance \(128\times 128\) squares) and apply the previous denoising method to all rectangles before reconstructing the whole image. Propose a solution to manage the overlapping areas.
3 DCT-based denoising
In the previous approach, the PCA basis can be replaced by a DCT orthogonal basis. All the coefficients smaller than a given threshold \(h\) in this basis are replaced by 0. See also the following IPOL demo : Guoshen Yu, and Guillermo Sapiro, DCT image denoising: a simple and effective image denoising algorithm, Image Processing On Line, 1 (2011).
The DCT thresholding denoising works better with larger patches (typically 15x15). If the following computations are too slow on your computer, try with a smaller image.
f = 7 b = im2col(u,[2*f+1 2*f+1],'sliding'); % matrix containing all patches as columns h = 3*sigma; b2d = reshape(b,2*f+1,2*f+1,size(b,2)); % reshape b into a stack of patches respatch = zeros(size(b)); nb = zeros(size(b)); for k=1:size(b,2) tmp = dct2(b2d(:,:,k)); % dct2 applied to each layer of b (each patch of u) tmp = tmp.*(tmp>h); % threshold the dct coefficients respatch(:,k) = reshape(idct2(tmp),(2*f+1)*(2*f+1),1); end
Reconstruct the final result by
res = zeros([size(uo),(2*f+1)^2]); weight = zeros([size(uo),(2*f+1)^2]); for i = 1:(2*f+1) for j = 1:2*f+1 k = i+(2*f+1)*(j-1); res(i:end-2*f-1+i,j:end-2*f-1+j,k) = reshape(respatch(k,:),size(u,1) - 2*f,size(u,2) - 2*f); weight(i:end-2*f-1+i,j:end-2*f-1+j,k) = 1; end end resweight = sum(res.*weight,3)./sum(weight,3); figure;imshow(resweight,[]);

Figure 6 : Image restored by projecting the noisy image on the DCT basis and thresholding the DCT coefficients smaller than 3*sigma