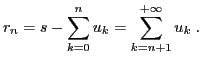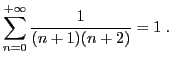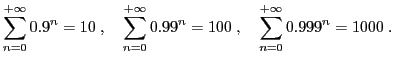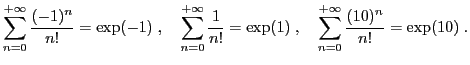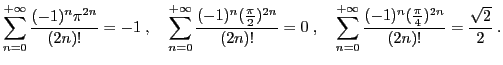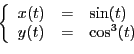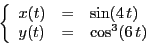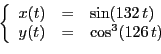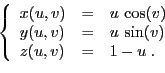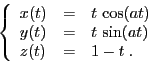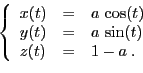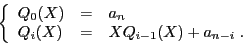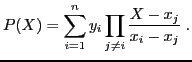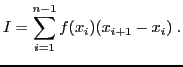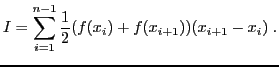suivant: QCM corrigés
monter: CN_ECS
précédent: Calcul numérique
Table des matières
Index
Il y a souvent plusieurs manières d'obtenir le même résultat en
Scilab. On s'efforcera de choisir les solutions les plus compactes,
c'est-à-dire celles qui utilisent au mieux le langage matriciel.
Exercice 1 Écrire (sans utiliser de boucle) les vecteurs suivants :
- Nombres de
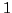 à
à 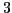 par pas de
par pas de 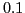 .
.
- Nombres de
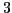 à
à 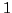 par pas de
par pas de 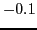 .
.
- Carrés des
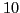 premiers entiers.
premiers entiers.
- Nombres de la forme
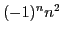 pour
pour
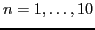 .
.
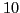 ``0
'' suivis de
``0
'' suivis de 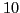 ``
``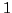 ''.
''.
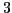 ``0
'' suivis de
``0
'' suivis de 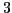 ``
``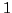 '', suivis de
'', suivis de 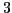 ``
``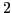 '',...,
suivis de
'',...,
suivis de 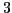 ``
``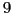 ''.
''.
- ``
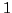 '', suivi de
'', suivi de 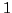 ``0'', suivi de ``2'', suivi de 2 ``0
'',...
, suivi de ``
``0'', suivi de ``2'', suivi de 2 ``0
'',...
, suivi de ``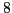 '', suivi de
'', suivi de 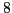 zéros, suivi de ``
zéros, suivi de ``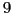 ''.
''.
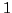 ``
``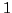 '' suivi de
'' suivi de 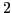 ``
``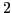 '', suivis de
'', suivis de 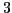 ``
``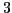 '',...,
suivis de
'',...,
suivis de 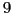 ``
``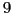 ''.
''.
Exercice 5
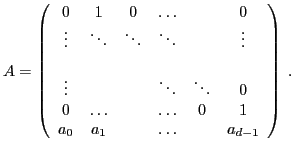
- Écrire la matrice carrée
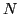 d'ordre
d'ordre 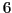 , telle que
, telle que 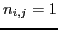 si
si 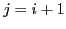 ,
0
sinon.
,
0
sinon.
- Calculer
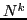 , pour
, pour
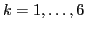 .
.
- Écrire la matrice
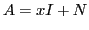 , où
, où 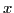 est une variable
de polynôme.
est une variable
de polynôme.
- Calculer
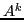 , pour
, pour
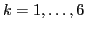 .
.
- Pour
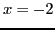 , et
, et 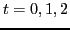 , calculer
, calculer 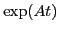 .
.
Exercice 6 Etant donnée une série numérique convergente
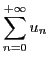
, de somme
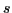
, le reste à l'ordre
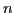
est défini comme la différence entre la somme et la somme
partielle à l'ordre
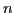
.
Le but de l'exercice est de déterminer la valeur de
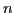
à partir
de laquelle le reste
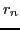
est inférieur à
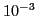
, pour les
séries suivantes.
-
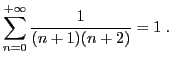
-
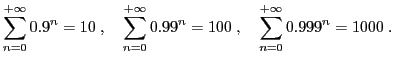
-
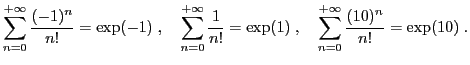
-
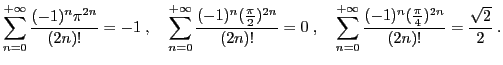
Exercice 9
- Représenter la fonction
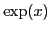 sur l'intervalle
sur l'intervalle ![$ [-1,1]$](img121.png) .
Sur le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en
.
Sur le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en 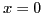 , aux ordres
, aux ordres
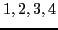 .
.
- Représenter la fonction
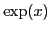 sur l'intervalle
sur l'intervalle ![$ [1,2]$](img124.png) .
Sur le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en
.
Sur le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en 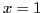 , aux ordres
, aux ordres
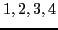 .
.
- Représenter la fonction
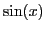 sur l'intervalle
sur l'intervalle
![$ [-\pi,\pi]$](img127.png) . Sur
le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en
. Sur
le même graphique, superposer les représentations
des polynômes de Taylor de cette fonction en 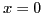 , aux ordres
, aux ordres
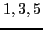 .
.
Exercice 12 Pour chacune des courbes paramétrées suivantes, on choisira un
intervalle de valeurs du paramètre et un pas de discrétisation
assurant une représentation complète et suffisamment lisse.
Exercice 14 Le but de l'exercice est de visualiser un cône de différentes
manières.
- Représenter la surface d'équation
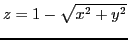 .
.
- Représenter la surface paramétrée définie par :
- Représenter la courbe paramétrée définie par :
(On choisira une valeur de 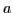 suffisamment grande).
suffisamment grande).
- Représenter la famille de courbes paramétrées définies par :
Exercice 19 Écrire les fonctions suivantes. Toutes prennent en entrée une fonction
externe
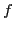
(de
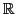
dans
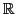
), et trois valeurs
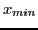
,
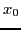
et
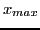
(supposées telles que
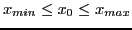
).
derive :
Elle calcule numériquement et représente graphiquement
la dérivée de 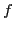 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img181.png) . Elle retourne la
valeur approchée de
. Elle retourne la
valeur approchée de 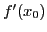 .
.
tangente :
Elle représente la fonction 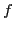 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img181.png) , elle
superpose sur le même graphique la tangente à
, elle
superpose sur le même graphique la tangente à 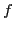 au point
au point 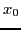 , et
retourne l'équation de cette tangente comme un polynôme du premier
degré.
, et
retourne l'équation de cette tangente comme un polynôme du premier
degré.
araignee :
Elle représente la fonction 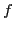 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img181.png) ,
ainsi que la droite d'équation
,
ainsi que la droite d'équation 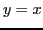 (première bissectrice).
Elle calcule et retourne les
(première bissectrice).
Elle calcule et retourne les 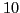 premiers itérés de
premiers itérés de 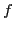 en
en 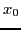 (
(
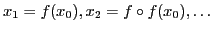 ). Elle représente la suite de
segments, alternativement verticaux et horizontaux, permettant de visualiser
les itérations : segments joignant
). Elle représente la suite de
segments, alternativement verticaux et horizontaux, permettant de visualiser
les itérations : segments joignant 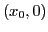 ,
, 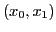 ,
, 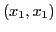 ,
,
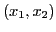 ,
, 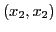 , ...
, ...
newton :
Elle représente la fonction 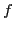 sur l'intervalle
sur l'intervalle
![$ [x_{min},x_{max}]$](img181.png) .
Elle calcule et retourne les dix premiers itérés de la suite définie
à partir de
.
Elle calcule et retourne les dix premiers itérés de la suite définie
à partir de 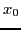 par la méthode de Newton :
par la méthode de Newton :
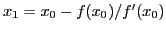 ,
,
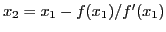 ... Les valeurs de la dérivée sont
approchées. La fonction représente sur le même graphique les
segments permettant de visualiser les itérations : segments joignant
... Les valeurs de la dérivée sont
approchées. La fonction représente sur le même graphique les
segments permettant de visualiser les itérations : segments joignant
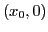 ,
,
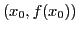 ,
, 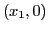 ,
,
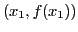 ,
, 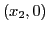 ,
,
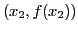 ,...
,...
Exercice 20 Soit
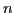
un entier,
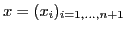
et
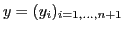
deux vecteurs de réels. On appelle
``polynôme interpolateur de Lagrange'' des
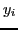
aux abscisses
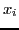
, le polynôme
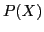
défini par :
- Écrire une fonction
poly_Lagrange, qui prend en entrée
deux vecteurs 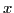 et
et 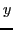 de meme taille.
Elle retourne le polynôme interpolateur de Lagrange
de meme taille.
Elle retourne le polynôme interpolateur de Lagrange 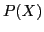 .
Elle represente sur le même graphique les points de coordonnées
.
Elle represente sur le même graphique les points de coordonnées
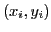 et le graphe du polynome
et le graphe du polynome 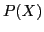 .
.
- Tester votre fonction avec :
x=[-5:5]; y=x.^2, puis y=x.^3-2*x.^2+4*x+1;
(verifier que y-horner(P,x) est proche de 0).
Tester votre fonction avec
plusieurs realisations de x=rand(1,10); y=rand(1,10);
Exercice 21
- Écrire une fonction
integre_rectangles qui prend en entrée un
vecteur
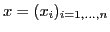 d'abscisses et un vecteur
d'abscisses et un vecteur
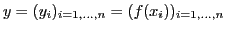 d'ordonnées et qui
calcule l'intégrale approchée de f par la méthode des rectangles
à gauche :
d'ordonnées et qui
calcule l'intégrale approchée de f par la méthode des rectangles
à gauche :
Comparer les résultats de cette fonction sur plusieurs intégrales,
calculées explicitement et avec les fonctions intrap
et intsplin.
- Même question avec la méthode des trapèzes :
Exercice 22
- L'intégrale de 0
à
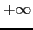 de
de
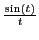 vaut
vaut
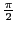 . Donner une representation graphique convaincante
de la fonction. Écrire une suite de commandes qui
permette de calculer l'intégrale avec une
précision de
. Donner une representation graphique convaincante
de la fonction. Écrire une suite de commandes qui
permette de calculer l'intégrale avec une
précision de 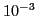 , avec chacune des fonctions
, avec chacune des fonctions
inttrap, intsplin integ et intg.
- Même question pour l'intégrale sur
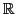 de
de
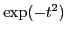 qui vaut
qui vaut
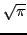 .
.
suivant: QCM corrigés
monter: CN_ECS
précédent: Calcul numérique
Table des matières
Index
Georges Koepfler
2011-01-19
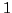 à
à 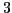 par pas de
par pas de 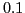 .
.
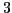 à
à 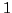 par pas de
par pas de 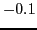 .
.
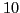 premiers entiers.
premiers entiers.
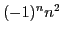 pour
pour
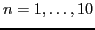 .
.
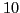 ``0
'' suivis de
``0
'' suivis de 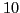 ``
``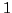 ''.
''.
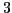 ``0
'' suivis de
``0
'' suivis de 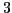 ``
``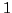 '', suivis de
'', suivis de 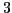 ``
``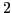 '',...,
suivis de
'',...,
suivis de 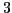 ``
``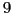 ''.
''.
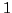 '', suivi de
'', suivi de 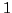 ``0'', suivi de ``2'', suivi de 2 ``0
'',...
, suivi de ``
``0'', suivi de ``2'', suivi de 2 ``0
'',...
, suivi de ``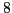 '', suivi de
'', suivi de 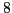 zéros, suivi de ``
zéros, suivi de ``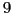 ''.
''.
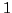 ``
``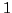 '' suivi de
'' suivi de 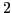 ``
``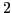 '', suivis de
'', suivis de 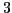 ``
``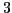 '',...,
suivis de
'',...,
suivis de 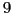 ``
``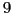 ''.
''.