Dans la ligne de l'idéologie quantitativiste, l'approche matricielle, actuellement dominante en statistique, ne connaît, pour caractériser et étudier les procédures statistiques, que les manipulations matricielles (opérations sur les tableaux de nombres). Si les formulations matricielles peuvent fournir une sténographie utile pour résumer les algorithmes des procédures, l'usage exclusif du calcul matriciel n'est pas assez puissant pour prendre en compte toutes les structures pertinentes; ce qui rend les développements particulièrement abscons voire incomplets, même dans les sentiers les plus battus de la statistique, comme la régression. En Analyse Géométrique des Données, la "présentation matricielle" de l'Analyse des Correspondances a abouti à la dégradation de la méthode. Voir Benzécri & al (1973, p.58) ; et Le Roux & Rouanet (2004, p. 9 et 449).
Critique de l'approche matricielle
S'il me fallait fournir un
seul "exemple concret"
des insuffisances de l'approche matricielle,
je donnerais l'exemple d'un plan d'expérience
de complexité modérée.
Voici donc comment le plan d'expérience (très
usuel) "sujets
S emboîtés dans le croisement de deux facteurs A et B " se
présente dans Kendall & Stuart (la "somme" de
la statistique
académique).
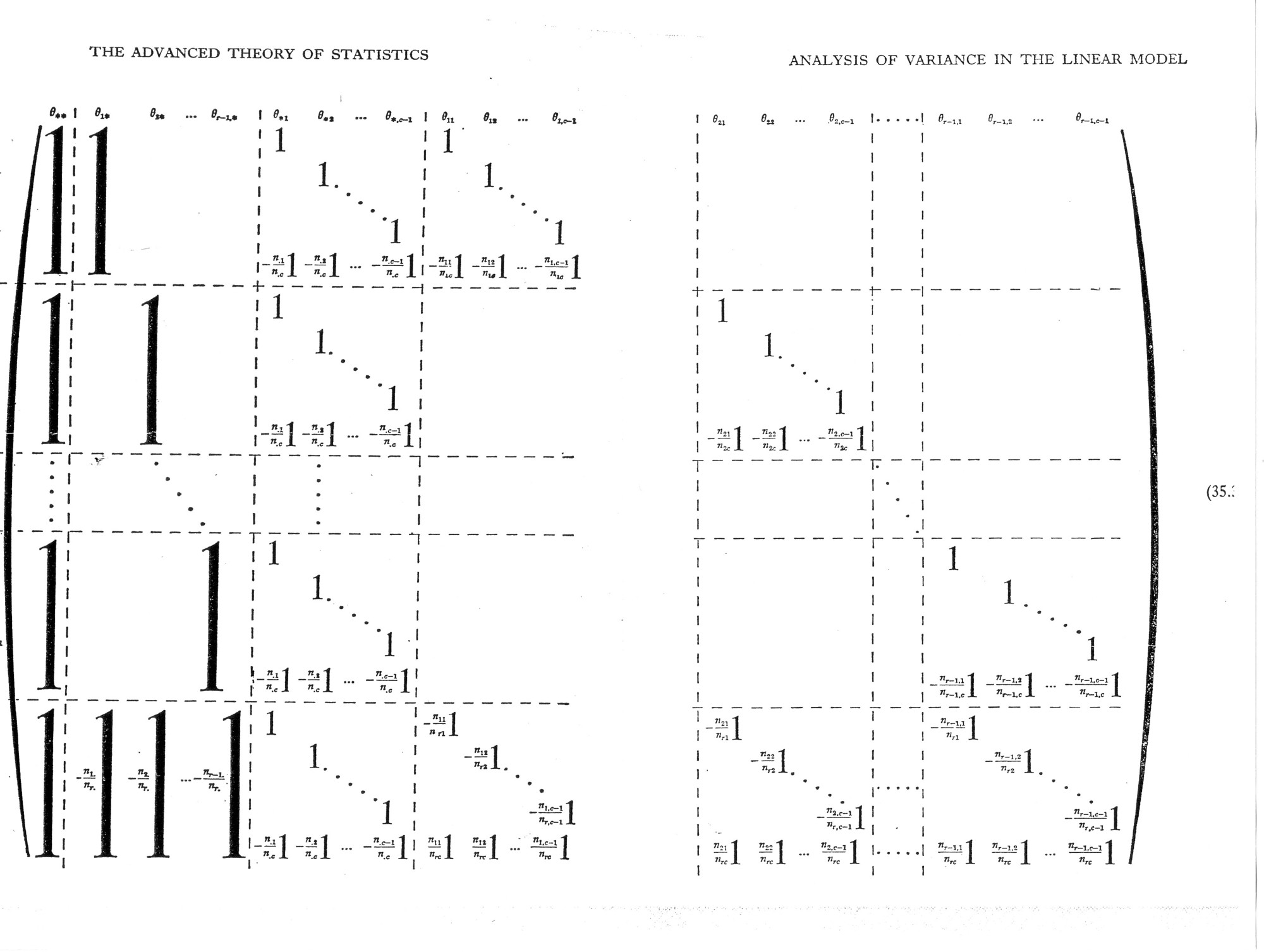

La formalisation des plans d'expérience renvoie naturellement aux structures ensemblistes..Dans la notation ensembliste que nous avons mise en oeuvre dans nos logiciels (VAR3, EyeLID), ce plan est noté S<A*B>. Cf. Analyse de Variance et Données Structurées
L'approche matricielle, au lieu de dégager les structures ensemblistes, les "traduit" à coup de "matrices en (0,1)". Des ouvrages entiers sont consacrés aux "propriétés des matrices en (0,1)", lesquelles sont en réalité des propriétés d'algèbre ensembliste, qui se traduisent très malaisément en langage matriciel.
Nous laissons au lecteur le soin d'imaginer la représentation matricielle des plans plus complexes, par exemple du plan "sujets S emboîtés dans le croisement de deux facteurs A et B et croisés avec deux autres facteurs" C et D, C étant emboîté dans D: plan que nous notons S<A*B>*C<D>...


La formalisation des plans d'expérience renvoie naturellement aux structures ensemblistes..Dans la notation ensembliste que nous avons mise en oeuvre dans nos logiciels (VAR3, EyeLID), ce plan est noté S<A*B>. Cf. Analyse de Variance et Données Structurées
L'approche matricielle, au lieu de dégager les structures ensemblistes, les "traduit" à coup de "matrices en (0,1)". Des ouvrages entiers sont consacrés aux "propriétés des matrices en (0,1)", lesquelles sont en réalité des propriétés d'algèbre ensembliste, qui se traduisent très malaisément en langage matriciel.
Nous laissons au lecteur le soin d'imaginer la représentation matricielle des plans plus complexes, par exemple du plan "sujets S emboîtés dans le croisement de deux facteurs A et B et croisés avec deux autres facteurs" C et D, C étant emboîté dans D: plan que nous notons S<A*B>*C<D>...