Abstract

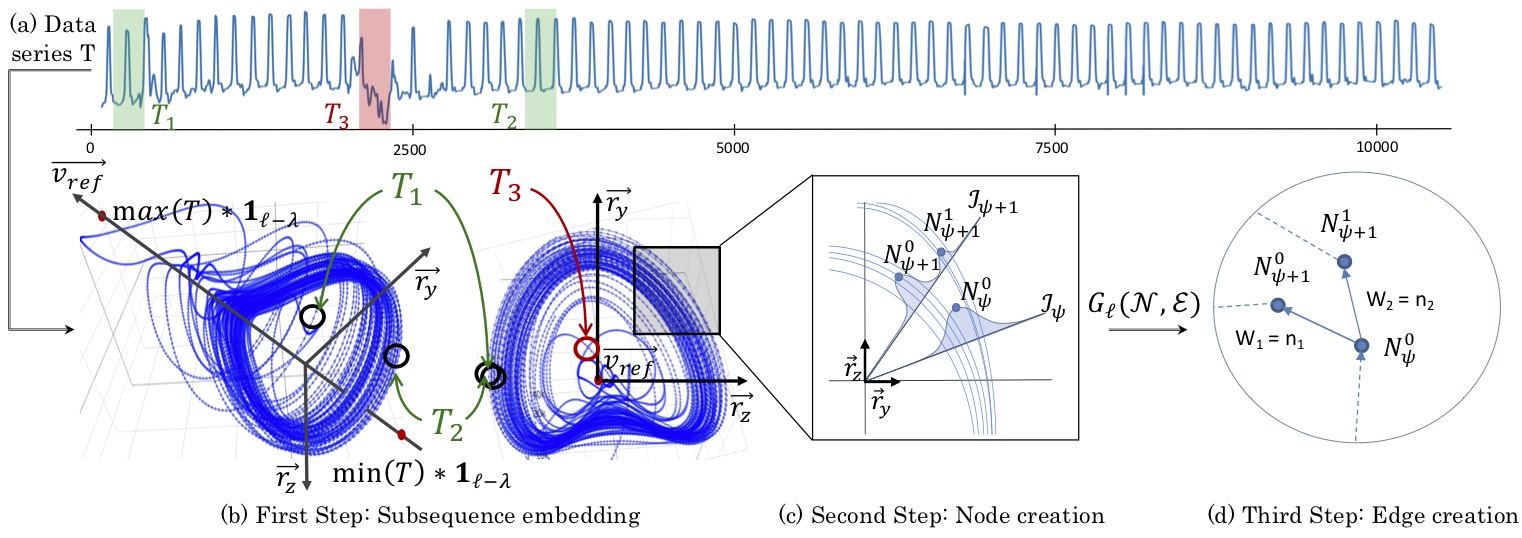
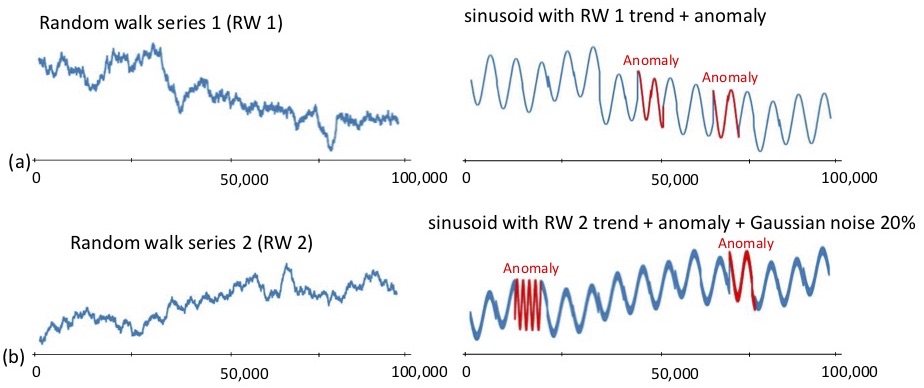
Subsequence anomaly detection in long sequences is an important problem with applications in a wide range of domains. However, the approaches that have been proposed so far in the literature have severe limitations: they either require prior domain knowledge that is used to design the anomaly discovery algorithms, or become cumbersome and expensive to use in situations with recurrent anomalies of the same type. In this work, we address these problems, and propose an unsupervised method suitable for domain agnostic subsequence anomaly detection. Our method, Series2Graph, is based on a graph representation of a novel low-dimensionality embedding of subsequences. Series2Graph needs neither labeled instances (like supervised techniques), nor anomaly-free data (like zero-positive learning techniques), and identifies anomalies of varying lengths. The experimental results, on the largest set of synthetic and real datasets used to date, demonstrate that the proposed approach correctly identifies single and recurrent anomalies without any prior knowledge of their characteristics, outperforming by a large margin several competing approaches in accuracy, while being up to orders of magnitude faster.

P. Boniol and T. Palpanas, Series2Graph: Graph-based Subsequence Anomaly Detection in Time Series, PVLDB (2020)

P. Boniol and T. Palpanas and M. Meftah and E. Remy, GraphAn: Graph-based Subsequence Anomaly Detection, demo PVLDB (2020)

Real Datasets

The real datasets we use in our study are the following:

Simulated engine disks data (SED) collected by the Rotary Dynamics Laboratory at NASA. This data series represents disk revolutions recorded over several runs (3K rpm speed).

MIT-BIH Supraventricular Arrhythmia Database (MBA), which are electrocardiogram recordings from 5 different patients, containing multiple instances of two different kinds of anomalies.

Five additional real datasets from various domains that have been studied in earlier works:

aerospace engineering: Space Shuttle Marotta Valve
gesture recognition: Ann’s Gun dataset
medicine: Patient’s respiration measured by the thorax extension and ECG recordings qtb/sel102
electrical consumption study: Dutch Power Consumption data

Synthetic Datasets

We use several synthetic datasets that contain sinusoid patterns at fixed frequency following a random walk trend (Figure 7). We then inject different numbers of anomalies, in the form of sinusoid waveforms with different phases and higher than normal frequencies, and add various levels of Gaussian noise on top. We refer to those datasets using the label SRW-[# of anomalies]-[% of noise]-[length of anomaly], and use them in order to test the performance of the algorithms under different, controlled conditions.

Source Code

Algorithms protected by patent. Code protected by copyright and provided as is. Email the authors for the password of the ZIP file. Users from the academia may use this code only for academic research purposes, provided that the authors are properly acknowledged by referencing the papers mentioned above. Users from the industry may test and evaluate this code by requesting a license.