suivant: Programmation
monter: CN_ECS
précédent: Vecteurs et matrices
Table des matières
Index
Sous-sections
Graphiques
Le principe général des représentations graphiques est de se ramener
à des calculs sur des matrices ou des vecteurs. Ainsi la représentation
d'une fonction de
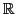 dans
dans
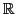 commencera par la création d'un vecteur
d'abscisses, en général régulièrement espacées, auxquelles on
applique la fonction pour créer le vecteur des ordonnées. Pour la
représentation d'une surface, il faudra créer la matrice des valeurs de
la fonction sur une grille rectangulaire dans
commencera par la création d'un vecteur
d'abscisses, en général régulièrement espacées, auxquelles on
applique la fonction pour créer le vecteur des ordonnées. Pour la
représentation d'une surface, il faudra créer la matrice des valeurs de
la fonction sur une grille rectangulaire dans
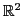 .
.
Il est impossible de décrire ici l'ensemble des fonctions graphiques et
leurs multiples options. Certaines de ces options, comme la numérotation
des couleurs, sont globales et peuvent être fixées par set (voir
help set).
Les démonstrations donnent une bonne idée
des possibilités graphiques de Scilab. On obtient en général
un exemple d'utilisation d'une fonction graphique en appelant cette fonction
à vide. L'interface graphique permet de zoomer sur
une partie d'un graphe 2D et d'effectuer des
rotations sur les images 3D à l'aide de la souris.
On ne présentera ici que les fonctions graphiques propres à Scilab,
depuis la version 4.1 il y a une plus grande compatibilité avec Matlab©
ce qui permet en particulier d'avoir des graphiques
en mode Matlab©, voir help plot.
Par défaut, les
graphiques successifs sont superposés sur la même fenêtre.
On efface la fenêtre courante par clf()
On ouvre la fenêtre
numéro i par scf(i).
On l'efface avec clf(i).
help Graphics
plot2d1()
clf()
histplot()
clf()
plot3d()
clf()
hist3d()
clf()
param3d()
Avec scf() on crée une nouvelle fenêtre graphique et
xdel(i) supprime la fenêtre numéro i.
clf()
plot2d1()
scf()
histplot()
scf()
plot3d()
clf(1) // efface la figure 1
scf(1) // la figure 1 est figure courante
hist3d()
xdel(winsid()) // supprime toutes les fenêtres graphiques ouvertes
La commande winsid() renvoie la liste des fenêtre graphiques ouvertes.
Le plus simple pour commencer est de tracer le graphe d'une fonction
de
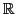 dans
dans
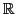 à l'aide de
à l'aide de plot2d. On crée pour cela un vecteur x d'abscisses,
et on prend l'image de ce vecteur par la fonction pour créer un vecteur
y d'ordonnées. La commande plot2d(x,y) représente les
points de coordonnées (x(i),y(i)) en les joignant par des
traits noirs (par défaut), ou selon un autre style, si le style de
base a été changé. La qualité de la représentation dépend
donc du nombre de points.
Note : la commande plot utilise la syntaxe Matlab©, ici on utilisera
de préférence la commande plot2d.
x=linspace(0,3*%pi,10); y=x.*sin(x);
plot2d(x,y)
clf() // sinon superposition
x=linspace(0,3*%pi,100); y=x.*sin(x);
plot2d(x,y)
On obtient le même résultat par fplot2d, mais
il faut pour cela prédéfinir la fonction à représenter.
Les tracés successifs se superposent.
deff("y=f(x)","y=x.*sin(x)")
x=linspace(0,3*%pi,10);
fplot2d(x,f) // ici on a superposition
x=linspace(0,3*%pi,100);
fplot2d(x,f)
Quand on veut superposer plusieurs courbes avec les mêmes échelles
de représentation, il
est préférable d'utiliser plot2d, qui autorise des styles
différents pour chaque courbe. La syntaxe générale est la
suivante.
plot2d(abscisses,ordonnees,[clef1=valeurs1 [,clef2=valeurs2]] )
Après les deux premiers, les arguments sont facultatifs,
les ``clefs'' indiquent les paramètres du graphique que l'on désire
fixer à ``valeurs'', voir la suite.
Signification des arguments :

abscisses, ordonnees :
Si ce sont des vecteurs (une seule courbe à tracer), ils peuvent être ligne ou colonne.
Si plusieurs courbes doivent être tracées, soit abscisses est un vecteur colonne
et ordonnees une matrice ayant le même nombre de lignes (i.e. nombre de points) et
un nombre de colonnes donné (i.e. le nombre de courbes) ;
soit ce sont des matrices de mêmes dimensions : à chaque vecteur colonne ``abscisse'' correspond
un vecteur colonne ``ordonnée'' de même taille.
Par défaut les points seront reliés par des segments.
A chaque courbe correspond une couleur de la palette, il y en a 32,
faire getcolor pour obtenir l'affichage de la palette.
x=linspace(0,3.5*%pi,30);
y=x.*sin(x);
plot2d(x,y)
clf()
y2=2*y;
plot2d([x,x],[y,y2]) // incorrect : deux courbes concatenees
clf()
plot2d([x;x],[y;y2]) // incorrect : trace 30 segments
clf()
plot2d([x;x]',[y;y2]') // correct
clf()
plot2d(x',[y;y2]') // correct
clf()
X=x'*ones(1,20);
Y=y'*[1:20];
plot2d(X,Y)
Les clefs et une partie des valeurs possibles sont présentées ci-dessous,
sous la forme clef=valeur .
Pour plus de détails se référer à l'aide en ligne de plot2d.

style=vect_style : vect_style
est un vecteur ligne dont la dimension
est le nombre de courbes à tracer (nombre de colonnes des matrices
abscisses et ordonnees). Les coordonnées sont
positives ou négatives. Si le style est positif, les points sont
joints par des segments. Si le style est nul, les points sont
affichés comme des pixels noirs. Si le style est négatif, des
marques de formes particulières sont affichées.
x=linspace(0,3*%pi,30); X=x'*ones(1,10);
y=x.*sin(x); Y=y'*[1:10];
couleurs=matrix([2;5]*ones(1,5),1,10)
clf()
plot2d(X,Y,style=couleurs)
marques=-[0:9]
clf()
plot2d(X,Y,style=marques)

rect=vect_rect : vect_rect est le rectangle de
représentation, décrit par les deux coordonnées du coin
inférieur gauche, suivies des deux coordonnées du coin supérieur
droit : [xmin,ymin,xmax,ymax].
x=linspace(0,3*%pi,30);
y=x.*sin(x);
clf()
plot2d(x,y)
scf()
plot2d(x,y,rect=[0,-10,9.5,10])

frameflag=int_ff : int_ff est un
entier entre 0 et 8 qui code le calcul des échelles en abscisse et ordonnée.
Pour frameflag=0 on utilise les échelles du graphique précédent ;
pour frameflag=1 on calcule les échelles grâce à vect_rect ;
pour frameflag=2 on détermine les échelles optimales à partir des données
abscisses, ordonnees.
pour frameflag=6 on détermine les échelles optimales à partir des données
abscisses, ordonnees mais de façon à avoir de
``jolies'' graduations.

axesflag=int_ax : int_ax est un
entier entre 0 et 5 qui code le tracé des axes et du cadre.
Pour axesflag=0 rien n'est tracé ;
pour axesflag=1 on trace les axes, les ordonnées sont à gauche ;
Pour axesflag=2 on trace juste un cadre autour du graphe.
x=linspace(0,3*%pi,30);
y=x.*sin(x);
clf()
plot2d(x,y)
y2=2*y;
plot2d(x,y2,style=2) // échelles différentes adaptées
scf()
plot2d(x,y)
plot2d(x,y2,style=2,axesflag=0, frameflag=0) // on utilise les axes précédents
scf()
plot2d(x,y2,style=2)
plot2d(x,y,axesflag=0, frameflag=0) // on utilise les axes précédents

leg=legendes : c'est une chaîne de
caractères contenant les différentes légendes, séparées par
@.
x=linspace(0,3*%pi,30); X=x'*ones(1,5);
y=x.*sin(x); Y=y'*[1:5];
vect_styles=[-2:2]
legendes="x sin(x)@2 x sin(x)@3 x sin(x)@4 x sin(x)@5 x sin(x)"
clf()
plot2d(X,Y,style=vect_styles,leg=legendes)
scf() // meme affichage
plot2d(X,Y,style=vect_styles, frameflag=6, axesflag=1,leg=legendes)
Les commandes captions et legend sont plus flexibles et à préférer.

nax=graduations : graduations est un
vecteur de quatre entiers qui
permet de préciser le nombre des graduations et
sous-graduations en abscisse et ordonnée. Par exemple, avec
[4,11,4,5],
l'intervalle des abscisses sera divisé en 10 intervalles,
i.e. 11 graduations,
chacun des 10 intervalles étant subdivisé par 4 sous-graduations, i.e.
5 sous-intervalles. Pour les ordonnées il y aura 4
intervalles, chacun subdivisé en 5 sous-intervalles.
x=linspace(0,3*%pi,30);
y=x.*sin(x);
clf()
plot2d(x,y, rect=[0,-10,10,10])
scf()
plot2d(x,y, rect=[0,-10,10,10],nax=[4,11,4,5])

logflag=ch_log : ch_log est une chaîne de deux caractères parmi :
"nn" (défaut), "nl", "ln" et "ll",
où n indique l'échelle habituelle, tandis que l indique que l'on utilise
une échelle logarithmique. Ainsi logflag="nl" utilise en abscisse l'échelle normale
et en ordonnée l'échelle logarithmique.
N=[2:100000]';
C1=N.*log(N);
C2=N.^2;
clf()
plot2d(N,[ C1 C2],style=[2,3],leg="N ln(N) @ N^2" )
scf()
plot2d(N,[ C1 C2],style=[2,3], logflag="ll",leg="N ln(N) @ N^2")
Dans l'ancienne syntaxe de la commande plot2d,
syntaxe que l'on tachera d'éviter,
on n'avait pas besoin de préciser le clef si on gardait un certain ordre.
Dans ce cas, si l'un des arguments est précisé,
ceux qui le précèdent devront l'être aussi.
On peut trouver une description en ligne grâce à
help plot2d_old_version.
Figure 1:
Représentation de plusieurs courbes.
|
|
| Graphes de fonctions |
plotframe |
rectangle de représentation |
plot2d |
plusieurs courbes avec styles différents |
plot2d1 |
idem, avec plus d'options |
plot2d2 |
représentation en escalier |
plot2d3 |
barres verticales |
plot2d4 |
flèches |
fplot2d |
représenter des fonctions |
Les échelles de représentation, choisies automatiquement, ne sont
pas les mêmes en abscisse et en ordonnée. On peut corriger ceci
grâce à l'option frameflag de plot2d ou
à l'aide des commandes isoview et square.
Remarque : Cette section n'a pas été mise à jour. On y utilise des commandes
obsolètes depuis la version 5.1 (p. ex. xset) mais sont encore
utilisables avec la 5.1.1. En attendant l'installation de la 5.2
et afin d'illustrer quelques possibilités graphiques de Scilab, on a gardé les exemples tels quels.
Si une même représentation graphique comporte plusieurs tracés
à des échelles différentes, on peut spécifier d'abord
le rectangle de représentation et les échelles des axes par
plotframe, pour ensuite superposer les différents tracés.
La clef rect est la même que pour plot2d, tandis
que tics correspond à nax et captions à
leg.
clf();
xset("font",2,4);
plotframe(rect=[-4,-1,4,1],tics=[2,9,5,10],captions=["Titre","Axe x","Axe y"])
x=linspace(-%pi,%pi,50); y=sin(x);
plot2d(x,y); // trace une courbe
x=linspace(-%pi/2,%pi/2,5); y=sin(x);
xset("mark",1,2);
plot2d(x,y,style=-3, frameflag=0); // affiche 5 marques
x=linspace(-%pi,%pi,20); y=sin(x)/2;
xset("use color",1);
xset("pattern",13);
xfpoly(x,y); // surface remplie
Figure 2:
Figure composée.
|
|
Il est fréquent qu'un graphique contienne non seulement une ou plusieurs
représentations de fonctions, mais aussi des chaînes de
caractères, des rectangles, ellipses ou autres ajouts graphiques.
Les coordonnées de ces ajouts sont relatives à la fenêtre
courante. Là aussi, on pourra spécifier le cadre
au préalable par plotframe.
clf()
plotframe(rect=[-1,0,2,4],tics=[10,3,5,4],captions=["Parabole","x","f(x)"])
x=linspace(-1,2,100); y=x.*x;
plot2d(x,y,style=2) // represente la courbe
plot2d([1,1,-1],[0,1,1],style=3) // trace deux segments
help xstring
xstring(1.1,0.1,"abscisse") // chaine de caracteres
xstring(-0.9,1.1,"ordonnee") // autre chaine
help xarc
xarc(-0.5,1,1,1,0,360*64) // trace un cercle
Figure 3:
Figure composée.
|
|
| Ajouts sur graphique |
xarc |
arc d'ellipse |
xfarc |
arc d'ellipse plein |
xarrows |
flèches |
xnumb |
nombres |
xpoly |
polygone |
xfpoly |
polygone plein |
xrpoly |
polygone régulier |
xrect |
rectangle |
xfrect |
rectangle plein |
xstring |
chaîne de caractères (à partir d'un point) |
xstringb |
chaîne de caractères (dans un rectangle) |
xtitle |
titre du graphique et des axes |
Des fonctions prédéfinies permettent d'effectuer des
représentations planes particulières, comme des histogrammes,
des projections de surfaces par courbes de niveau ou niveaux de gris, ou des
champs de vecteurs. Les exemples qui suivent concernent la fonction de
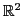 dans
dans
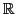 qui à
qui à 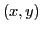 associe
associe 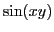 (voir figures
4, 5 et 6).
(voir figures
4, 5 et 6).
//
// Courbes de niveau
//
x=linspace(-%pi,%pi,50); // vecteur d'abscisses
y=x; // vecteur d'ordonnees
z=sin(x'*y); // matrice des valeurs de la fonction
help contour2d
clf()
contour2d(x,y,z,4) // trace 4 courbes de niveau
//
// Surface par niveaux de couleurs
//
clf()
grayplot(x,y,z) // pas vraiment gray le plot
clf()
R=[0:255]/256; G=R; B=R;
RGB=[R;G;B]'; // nouvelle matrice de couleurs
xset("colormap",RGB);
grayplot(x,y,z) // niveaux de gris
//
// Champ de vecteurs tangents
//
xset("default") // reinitialise les parametres graphiques
x=linspace(-%pi,%pi,10); // vecteur d'abscisses
y=x; // vecteur d'ordonnees
fx=cos(x'*y)*diag(y); // matrice des abscisses de vecteurs
fy=diag(x)*cos(x'*y); // matrice des ordonnees de vecteurs
champ(x,y,fx,fy) // champ des vecteurs
Figure 4:
Représentation par courbes de niveau.
|
|
Figure 5:
Représentation par niveaux de gris.
|
|
Figure 6:
Représentation d'un champ de vecteurs.
|
|
| Représentations planes particulières |
histplot |
histogramme |
champ |
champ de vecteurs |
fchamp |
idem, définition par une fonction |
grayplot |
surface par rectangles de couleurs |
fgrayplot |
idem, définition par une fonction |
contour2d |
courbes de niveaux projetées |
fcontour2d |
idem, définition par une fonction |
Le tracé d'une courbe en dimension 3 se fait par la fonction
param3d, selon les mêmes principes qu'en dimension 2.
clf()
t=linspace(0,2*%pi,50);
x=sin(t); y=sin(2*t); z=sin(3*t);
param3d(x,y,z) // courbe de Lissajous
scf() // nouvelle fenêtre
t=linspace(-%pi/2,%pi/2,1000);
x=cos(t*50).*cos(t);
y=sin(t*50).*cos(t);
z=sin(t);
param3d(x,y,z) // helice spherique
Pour représenter une famille de courbes en dimension 3, il faut
utiliser param3d1. Les arguments sont trois matrices de
coordonnées pour lesquelles les différentes courbes sont en colonne.
clf()
t=linspace(0,2*%pi,100);
a=linspace(-%pi,%pi,10);
X=cos(t')*cos(a); // matrice des abscisses
Y=sin(t')*cos(a); // matrice des ordonnees
Z=ones(t')*sin(a); // matrice des cotes
param3d1(X,Y,Z) // paralleles d'une sphere
La représentation des surfaces se fait par plot3d ou
plot3d1. Nous reprenons comme exemple la fonction de
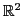 dans
dans
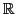 qui à
qui à 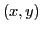 associe
associe 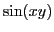 (figure 7).
(figure 7).
x=linspace(-%pi,%pi,50); // vecteur d'abscisses
y=x; // vecteur d'ordonnees
z=sin(x'*y); // matrice des valeurs de la fonction
help plot3d
clf()
plot3d(x,y,z) // representation monochrome
plot3d1(x,y,z) // representation coloree
scf()
R=[0:255]/256; G=R; B=0.5*ones(R);
RGB=[R;G;B]'; // nouvelle matrice de couleurs
xset("colormap",RGB);
plot3d1(x,y,z) // les couleurs dependent de z
xset("default") // reinitialise les parametres graphiques
Pour représenter une surface définie par deux paramètres, il
faut la définir comme une fonction, puis utiliser eval3dp
qui prend comme argument cette fonction et deux vecteurs de
paramètres, et retourne les arguments nécessaires pour la
représentation par plot3d. Voici par
exemple la représentation d'une sphère. Pour obtenir des couleurs
variables, il faut parfois changer le sens d'un des deux vecteurs de
paramètres.
deff("[x,y,z]=sphere(u,v)",.. // definition de la fonction
["x=cos(u).*cos(v);.. // abscisses
y=sin(u).*cos(v);.. // ordonnees
z=sin(v)"]) // cotes
u = linspace(-%pi,%pi,50);
v = linspace(-%pi/2,%pi/2,25);// parametres
[x,y,z] = eval3dp(sphere,u,v);// calcul de la surface
plot3d1(x,y,z); // representation monochrome
u = linspace(%pi,-%pi,50); // changement de sens
[x,y,z] = eval3dp(sphere,u,v);// nouveau calcul
scf()
plot3d1(x,y,z) // les couleurs dependent de z
Figure 7:
Représentation par plot3d1.
|
|
| Dimension 3 |
param3d |
courbes paramétriques |
param3d1 |
plusieurs courbes ou points |
plot3d |
surface en dimension 3 |
fplot3d |
idem, définition par une fonction |
plot3d1 |
surface par niveaux de couleurs |
fplot3d1 |
idem, définition par une fonction |
eval3dp |
surface paramétrée |
hist3d |
histogrammes |
suivant: Programmation
monter: CN_ECS
précédent: Vecteurs et matrices
Table des matières
Index
Georges Koepfler
2011-01-19
![\includegraphics[width=10cm]{xsinx_courbes.eps}](img34.png)
![\includegraphics[width=10cm]{sinx_compose.eps}](img35.png)
![\includegraphics[width=10cm]{parabole_compose.eps}](img36.png)
![\includegraphics[width=10cm]{sinxy_contour.eps}](img39.png)
![\includegraphics[width=10cm]{sinxy_gris.eps}](img40.png)
![\includegraphics[width=10cm]{sinxy_champ.eps}](img41.png)
![\includegraphics[width=10cm]{sinxy_surf.eps}](img42.png)