DOMAINES 

1. Modèles stochastiques d'apprentissage   
2. Analyse de la variance & Données structurées
3. Inférence  Combinatoire - Test du hasard
4. Inférence bayésienne - Inférence fiduciaire
5. Analyse Géométrique  des données
6. Régression

INFERENCE BAYESIENNE

DIalogue de sourds

 Le cadre bayésien

Dans le cadre bayésien, la probabilité retrouve  sa sémantique  naturelle:  évaluer l'incertitude allant  du connu (les données statistiques) vers  l'inconnu (les hypothèses d'intérêt). Moyennant  une  distribution initiale qui synthétise les  informations autres que les données,  la formule  de Bayes conduit à une distribution finale qui permet de calculer les probabilités des hypothèses.

Après une longue traversée du désert, le cadre bayésien est aujourd'hui largement reconnu.  Alors que  dans l'édition de 1977 en trois tomes  de la "somme statistique" de  Kendall & Stuart,   la  référence à de Finetti (le plus éminent représentant  de l'inférence bayésienne) ne figurait même pas à l'index, aujourd'hui  dans la  série Kendall's Advanced Theory of Statistics,  un volume entier (Volume 2B) est entièrement consacré à la statistique bayésienne, avec cette tranquille déclaration préliminaire: "The Bayesian approach to statistics is now widely accepted as theoretically sound and practically viable".  On dénombre   1800 noms dans la "liste de Bernardo" en 2005  [Le statisticien espagnol José M.  Bernardo,  pionnier de la statistique bayésienne, rassemble  tous les quatre ans à Valence la communauté bayésienne]. On peut dire que  la révolution bayésienne est en marche, au moins en statistique académique!

Analyse Bayésienne des Données

En inférence bayésienne, le choix crucial est celui de la distribution initiale.  Lorsqu'on souhaite dissocier l'apport des données de celui des croyances initiales,  comme c'est le cas dans l'approche d'analyse des données, il faut choisir  une distribution  qui ne  reflète pas ces croyances, mais qui au contraire exprime une attitude neutre ou "non-informative";  la distribution finale  exprime alors  l'apport propre des données: on obtient ainsi,  dans  la tradition de Laplace à Jeffreys, l'Analyse  Bayésienne des Données. L'Analyse Bayésienne des Données réalise le plus complètement la démarche descriptive-inductive. Loin de s'opposer à l'inférence traditionnelle des chercheurs, elle en constitue   un prolongement.

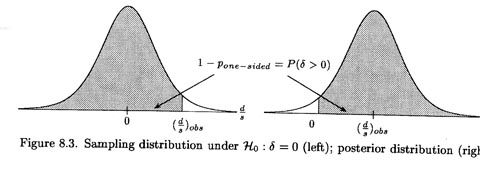
La réinterprétation  laplacienne du seuil  observé

Il s'agit  d'un résultat fondamental  de l'Analyse Bayésienne des Données, pour les modèles d'échantillonnage usuels. Ainsi dans la situation de comparaison de deux moyennes (figure): A gauche est représentée la distribution d'échantillonnage de la différence des moyennes; à droite, la distribution finale; cette dernière est  obtenue par translation de la précédente. Le seuil observé unilatéral de l'hypothèse nulle d'absence d'effet (delta=0) se réinterprète ainsi  comme  la probabilité que l'effet vrai delta  soit de sens opposé à l'effet observé dobs. Exemple: si l'effet observé dobs est positif, et s'il est juste significatif au seuil unilatéral .025 (i.e. seuil bilatéral p=.05), la probabilité bayésienne que l'effet vrai delta soit négatif  est .025,  donc  la probabilité bayésienne que l'effet vrai delta soit positif est 1- .025 = .975.

Problématique de l'effet notable /et de l'effet négligeable

Le résultat précédent est la clef de notre apport méthodologiquement le plus important dans le domaine: les procédures bayésiennes permettent de conduire à des  conclusions d'effet notable,  ou d'effet négligeable.

Dans l'étude de  de cas "Psychométrie": Rouanet, Lépine, Pelnard-Considère (1976b) [Extrait], reprise dans Rouanet (2000c), nous avons confronté les conclusions bayésiennes avec  les résultats des procédures traditionnelles. Lla confrontation est édifiante. On a 14 effets significatifs, mais  seulement  9  conclusions d'effet notable; et 9 effets non-significatifs, mais seulement 2 conclusions d'effet négligeable.

L'analyse bayésienne des données dans nos  travaux

Dans la ligne des travaux des années 1970, nombre  de travaux bayésiens ont été effectués dans le cadre du Groupe Mathématiques & Psychologie (GMP) dans les années 1980. Nous commentons ci-après quelques jalons, en liaison avec la bibliographe thématique.
 
.  Hoc (1983) [Préface] et B. Lecoutre  (1984) [Extraits de la Préface]. Ces ouvrages  exposent   en détail les approches fiducio-bayésienne et bayésienne  en analyse de variance.
.  Rouanet & Lecoutre (1983). Justification bayésienne de l'inférence  spécifique.
.   Bernard (1983,  Thèse de 3ème cycle). Inférence bayésienne sur des fréquences dans le cas de données structurées: méthodes exactes et approchées.
.  Bernard (1998, in  Rouanet & al: New Ways etc., Peter Lang). Bayesian inference for categorical data. Voir SIRS97RP et SIRS97. Ce chapitre peut être lu comme une introduction générale à l'Analyse  Bayésienne des Données. 
. Bernard, Blancheteau  & Rouanet  (1985) [Résumé]:  analyse  de données séquentielles.Texte de l'exposé de Cambridge: New ways of analysing sequences of actions.

 Bernard & al. (1999): l'analyse implicative bayésienne, Mathématiques & Sciences Humaines.
. Rouanet (1996). Le premier article bayésien dans la revue Psychological Bulletin depuis les années 1960. 

 . Rouanet, Bernard, B. Lecoutre, M.P. Lecoutre, Le Roux (1998) (avec le Dialogue  en ouverture). Synthèse des travaux bayésiens du GMP.
  . Le Roux & Rouanet (2004). Inférence bayésienne en Analyse Géométrique des Données; avec les études de cas "Parkinson" et "Espace politique". 

L'esprit humain est-il bayésien?

Cette question  est un thème de psychologie cognitive, que j'avais  abordé dès mon premier travail de recherche (Rouanet, 1961), précurseur des travaux anglo-saxons  sur le "neglect of  base rates" des années 1960 et 1970.  Tous les travaux en la matière montrent  bien que l'esprit humain   apprend par l'expérience en  s'efforçant de combiner les informations "expérimentales" avec celles "a priori",  et en percevant bien les situations où les deux sortes d'information sont conflictuelles.  Les travaux de M.P. Lecoutre et de  Durand (thèse de 1989) ont  montré que lorsque une question prédictive est posée en  termes d'une statistique naturelle ("Quelle est la probabilité qu'on retrouve une moyenne  de même signe si le résultat est significatif?"), les réponses des chercheurs (psychologues expérimentalistes)  sont en gros d'accord avec les estimations bayésiennes; alors que  lorsque la question est posée en termes du test de signification ("Quelle est la probabilité qu'on retrouve un résultat significatif?"), les réponses sont aberrantes, reflétant  une absence de représentation intuitive de la situation: voir  M.P.  Lecoutre & Rouanet (1993). Ces résultats confirment amplement la conclusion de Rouanet (1998, p.26-27) que l'esprit humain n'est en aucun sens un "statisticien fréquentiste". 

 Et à propos, qu'en est-il des esprits animaux?  Le naturaliste S. J. Gould, quant à lui, a déclaré  un jour  que le comportement bayésien est une garantie de survie pour  les espèces...